学生能够提前接触计算机编程，不断地有人开始尝试用计算机编程思想来解决一系列的数学问题，本文通过使用C语言作为途径，利用计算机编程技术来解决高中数学题中有关于抛物线与直线的焦点的一系列相关问题。
1 抛物线与直线交点求解的数学模型
在高中数学的课本中，我们把在平面内，从定点到定直线的距离相等的点的轨迹称为抛物线。把其中的定点称为做抛物线的焦点，定直线叫做抛物线的准线。
再进一步的把抛物线的定义进行细化：抛物线是指平面内到一个定点F（焦点）和一条定直线L（准线）距离相等的点的轨迹。它还有许多的表示方法，例如参数表示，标准方程表示等等。它在几何光学和力学中也有着非常重要的用处。抛物线也是圆锥曲线的一种，即圆锥面与平行于某条母线的平面相截得到的曲线。
抛物线在合适的坐标变换下，也可看做成为二次函数图像。本文中我们用y=ax2+bx+c（a≠0，后续不再标明）作为抛物线的函数的通用数学式。在高中的数学课本书中经常会出现求抛物线与y=kx+d（k≠0，后续不再标注）的直线的交点的问题。本文将着重讨论通过计算机编程技术来处理y=ax2+bx+c的抛物线与y=kx+d的直线的交点的这一类问题。
抛物线y=ax2+bx+c与直线y=kx+d的交点的求法，就是将两边相等，变为ax2+bx+c=kx+d，继续变换为ax2+（b-k）x+（c-d）=0，由二次函数求解x的值。解二元一次方程可求解x，公式如下。
利用计算机编程技术来求解抛物线与直线的交点时，就是根据公式一来编写算法来求解抛物线和直线的交点。
2 计算机编程求解交点算法
计算机编程求解抛物线与直线交点的算法如下：
（1）获取抛物线方程中的x项的系数参数：a、b、c；
（2）获取直线方程中的想、项的系数参数：k、d；
（3）计算△的值；
（4）判断△的值与0的大小
（5）若△的值大于0，则根据公式一，计算x的两个值，并且说明抛物线与直线的有两个交点，打印出两个交点的（x，y）值；
（6）若△的值等于0，则根据公式一，计算x的唯一值，并且说明抛物线与直线只有一个交点，打印出一个交点的（x，y）值；
（7）若△的值小于0，则说明抛物线与直线没有
交点。
3 求解算法的设计与实现
3.1 流程设计
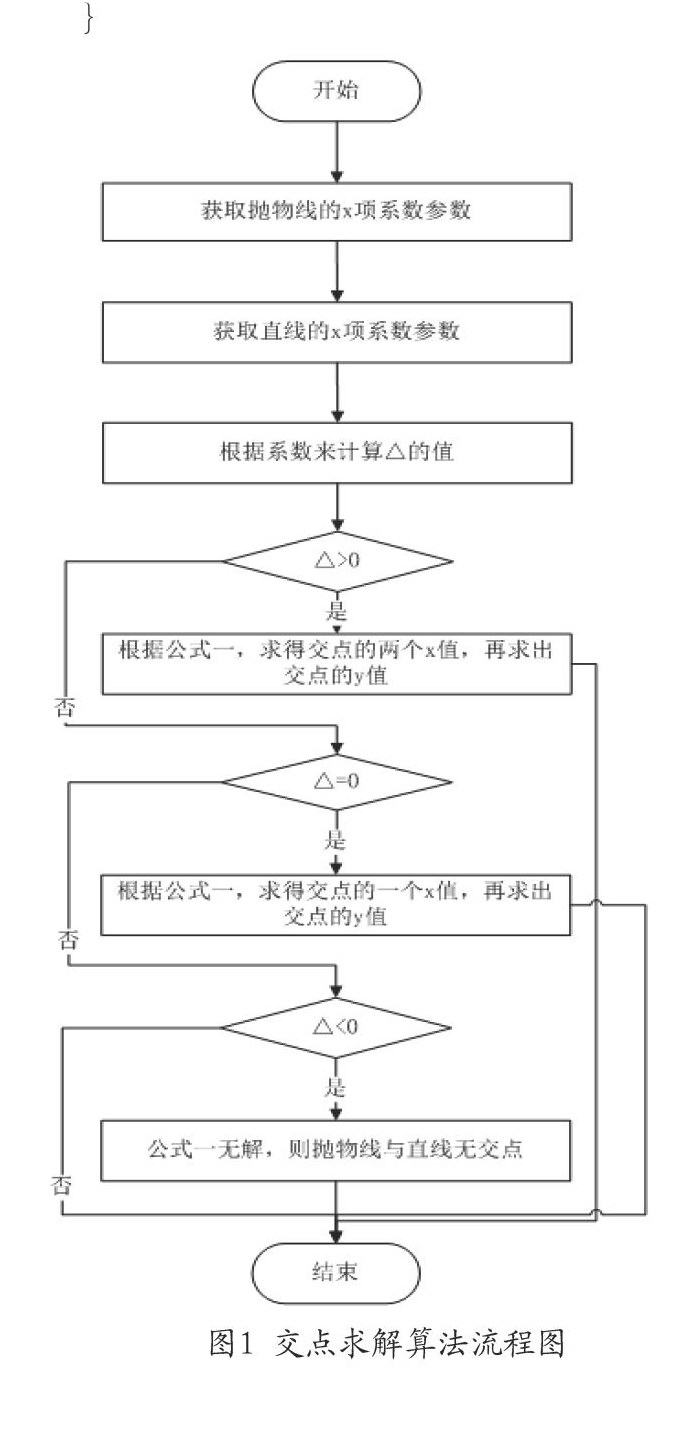
根据前文的求解算法，可画出抛物线与直线的交点求解算法的流程图，如图1所示。
3.2 算法编码
根据计算机编程求解交点算法和计算机编码求解交点的流程图，利用C语言编写的算法代码如下：
3.3 算法验证
为了验证上面介绍的计算机求解算法，我们在高中数学课本中随机的选择了如下的二次抛物线方程：
y = 2x2+6x+3；
与直线方程：
y = 2x+1；
利用公式一通过笔算可求得，二次抛物线与直线有一个交点，交点的（x，y）值是（-1，-1）；
上述二次抛物线方程的系数{a，b，c}={2，6，3}，直线方程的系数{k，d}={2，1}作为算法的参数输入程序。通过运算，可得二次抛物线与直线的交点结果，如图2所示。
由图2可知，抛物线与直线的交点只有一个交点是（-1.000000，-1.000000），与手算的结果一致。
4 总结
本文利用计算机编程，求解高中数学中的抛物线与直线的交点的数学问题。通过分析抛物线的基本特性，设计了算法流程，并使用C语言进行编码实现，最终通过一道实例验证了该算法的正确性。
参考文献
[1]邓世文.试论计算机技术在高中数学教学中的应用[J].实践与科学，2014（4）：12.
[2]程文娜.浅谈高中数学教学中的计算技术教学[J].教育教学论坛，2013（4）：34.
[3]魏恺.计算机技术在高中数学教学中的应用[G].张家口职业技术学院学报，2004，17（2）.