设计的影响，采用模糊隶属度函数描述农产品市场供需的不确定性，利用模糊数学规划方法，建立了农产品生产基地、配送中心、超市门店的三级两阶的农产品冷链物流网络的多目标模糊数学规划模型。此外，通过一个数值算例，使用遗传算法验证了模型的有效性，结果表明物流服务水平一定时，模糊可行度水平越高，农产品冷链物流总成本越高；当模糊可行度一定时，物流服务水平越高，农产品冷链物流总成本越大。
关键词：农产品冷链配送 不确定环境 网络设计 遗传算法
引言
近年来，农产品冷链物流作为物流业的新兴分支和潜在利润点，在国内迅速发展起来。随着我国农产品产量和需求连续多年稳步增长，电子商务的迅速发展和“互联网+”时代的来临，为我国冷链行业提供了巨大的机遇和挑战。由于冷链行业的外部环境发生改变，农产品冷链物流的运作与决策变得更加不确定，考虑冷链物流配送成本、降低貨运腐损度以及提高连锁超市门店满意度具有必要性和急迫性。因此，本文尝试在农产品市场供需不确定的环境下，建立一个考虑冷链物流总成本和物流配送服务水平的农产品冷链物流网络多目标优化模型。
目前，国内外学者关于农产品冷链物流网络设计的研究很少，且大多数仅在确定的环境下进行研究，基于不确定环境下的农产品冷链物流网络设计相对较少。Zhou 和Liu（2003）提出了不确定需求下的带有容量限制的设施选址分配问题，并结合算例分析进行验证；Omar Ahumada等人（2012）根据生鲜农产品的天气和需求不确定性建立了一个生产和销售的随机规划模型，用来确定生鲜农产品的分配方案；崔广彬、李一军（2007）研究了需求模糊的环境下，建立了集成化的物流配送中心选址优化模型；陈鑫、汪传旭等人（2011）以应急救援中心为研究对象，研究了受灾点需求模糊的环境上，建立以总运输成本最小为目标的选址优化模型；毕娅、李文锋（2011）在需求点的需求量随机的环境下，建立了供应链总成本最小化和配送中心覆盖率最大化的多目标的离散随机选址模型；陈鑫、汪传旭（2012）研究了应急救援中心的受灾点在需求模糊随机的情况下，建立了总运输成本最小化的单目标选址优化模型；周秀秀（2013）研究了需求模糊环境下的设备选址问题，并设计了混合智能优化算法求解；孙玮珊、杨斌（2014）研究了绿色物流中的需求、单位运输成本及单位碳排放量等不确定环境下，建立以物流总成本最小化和二氧化碳排放量最小化为双目标的模糊数学规划模型。
从前人研究可以看出，针对不确定环境下农产品冷链物流网络设计问题进行研究得较少，因此本文以生产基地-配送中心-连锁超市门店的三级两阶的农产品冷链配送网络，建立以配送总成本最小、连锁超市门店时间满意度最大和货运腐损度最小的多目标模糊数学规划模型进行研究。
农产品冷链物流网络模型构建
（一）问题描述及假设
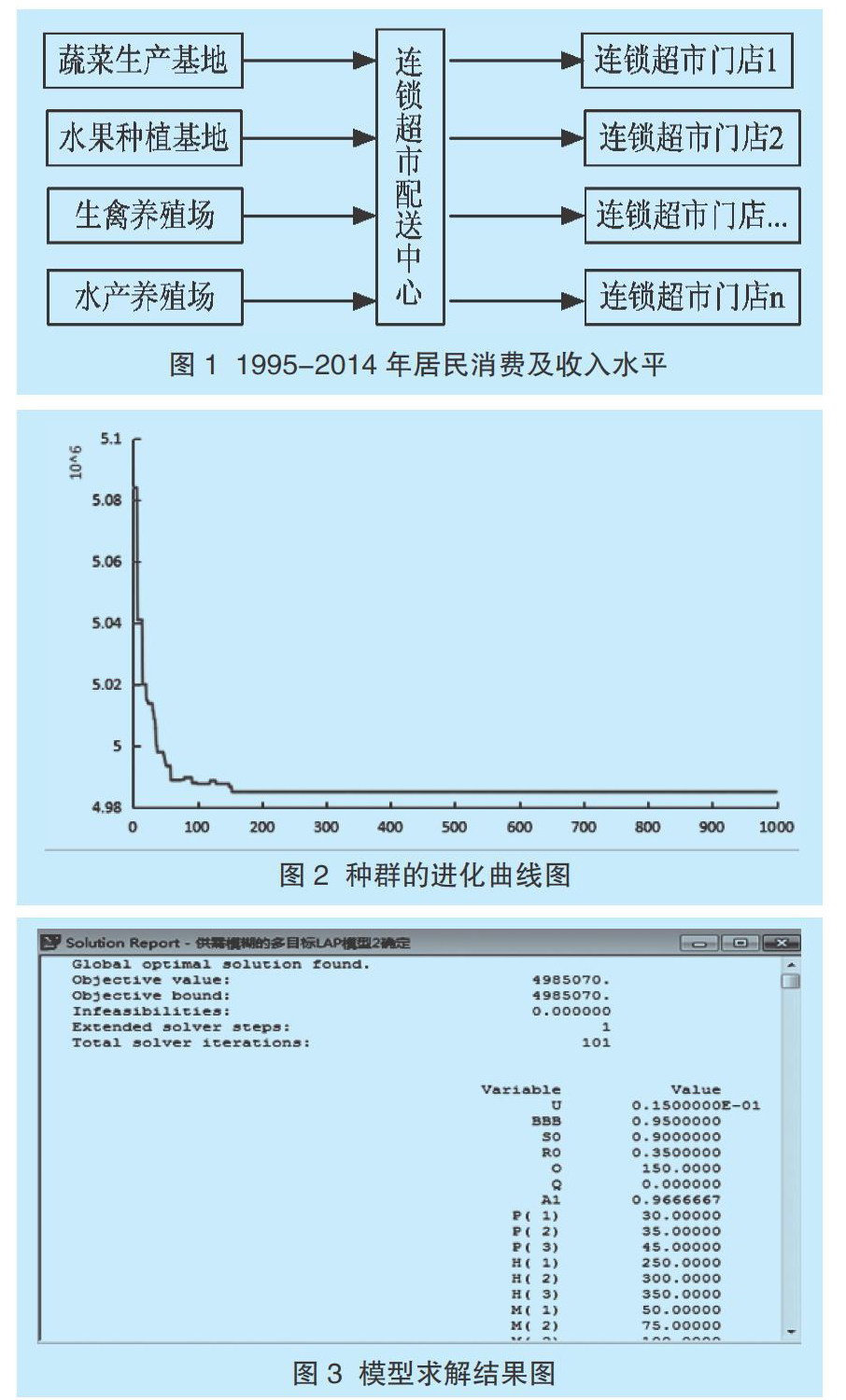
本文在理论基础上，考虑不确定环境下的连锁超市农产品冷链物流网络设计问题，研究了一体化的连锁超市农品冷链物流网络模式。如图1所示，这是个三级两阶多源多品种的连锁超市农产品冷链物流网络，其结构包括农产品生产基地、连锁超市配送中心及连锁超市门店3个层次。多源农产品生产基地供应多种类型的冷链农产品，在已有备选配送中心的基础上，选择其中的作为共同配送中心，负责向多个连锁超市门店进行配送，使得在满足各生产基地对各种产品的生产能力限制下和连锁超市门店对不同产品的时间窗要求下，以最少的物流配送总成本、最大的连锁超市门店满意度与最小的货运腐损度完成规定的配送业务。由于生鲜农产品具有易腐、生鲜的特性，为保持农产品的品质，需要在低温环境进行配送，因而会产生相应的冷藏成本与腐损成本。同时，由于各个连锁超市门店对各种农产品的配送时间窗要求，农产品的到达时间过早或过晚，会产生相应的仓储成本或惩罚成本。
根据上述问题，本文作出如下假设：生产基地的供应量和连锁超市门店的需求量不确定；连锁超市配送中心由于流通加工时间和管理费用较低，可以忽略不计；连锁超市门店每种农产品由一家连锁超市配送中心负责配送；连锁超市配送中心的容量和处理能力足够大，且备选地址已知；运输成本不受其它因素影响，只与单位运输成本和运输量成正比。
（二）模型参数与决策变量
1.下标。
N（v，a）表示连锁超市农产品冷链物流网络；I（1，2，…，i）表示农产品的种类；J（1，2，…，j）表示连锁超市配送中心的候选节点；K（1，2，…，k）表示连锁超市门店的数量；L（1，2，…，l）表示生产基地的数量。
2.决策变量。
xijl表示由第l个生产基地配送到第j个备选配送中心的第i种农产品的数量。
3.模型参数。
aijl表示由第l个生产基地到第j个备选配送中心的第i种产品的单位运输成本。
bik表示第k个连锁超市门店对第i种产品的需求量，是模糊变量。
cijk表示由第j个备选配送中心到第k个连锁超市门店的第i种产品单位运输成本。
dil表示第l个生产基地生产产品i的供应能力，是模糊变量。
tijk表示产品i从第j个备选配送中心到第k个连锁超市门店的实际配送时间。
[r1ik，s1ik]为硬时间窗，表示第k个连锁超市门店对第i种产品规定的配送时间窗。其中，r1ik为第k个连锁超市门店规定的产品i的最短配送时间，s1ik为第k个连锁超市门店规定的产品i的最长配送时间。
[r2ik，s2ik]为软时间窗，表示第k个连锁超市门店对第i种产品可接受的配送时间窗。其中r2ik为第k个连锁超市门店可接受的产品i的最短配送时间，s2ik为第k个连锁超市门店可接受的产品i的最长配送时间。
ej表示第j个配送中心的固定成本；f表示所需配送中心的数量；g表示单位时间的冷藏成本。
（三）目标函数
（二）多目标的处理
多目标决策方法主要有化多目标为单目标和分层序列等方法，其中多目标转化成单一目标有两种形式，一是附权重，二是考虑优先顺序，其具体几种较为常见的方法有主要目标法、线性加权法、理想点法、平方加权法和乘除法等。在这些方法中，线性加权、平方加权和理想点法需要目标函数的单位一致，而本文中的目标函数单位不同，分别是元和%，所以本文选择主要目标法来解决多目标数学模型。
引理3：针对一组设有m个目标f1（x），f2（x），…，fm（x），其中决策变量x∈X（约束集合），若以某个目标f1（x）为主要目标，并要求其为最优。对于其它目标只要使处于一定的数值范围内，如f`i（x）≤fi（x）≤f``i（x），i=2，3，…，m的问题可转化为如下单目标问题：
（三）遗传算法设计
遗传算法（GA，Genetic Algorithm）是美国学者霍兰德（J.Holland）于1975年提出的，这是一种模拟自然界中遗传学理论而建立的高效的全局搜索算法。遗传算法的优点包括全局搜索能力强和鲁棒性较好，以及適用于并行处理。
遗传算法采用的是迭代的运算方法，其具体运行过程和步骤如下所示：
将所要解决的问题域中的各个可能的结果确定为群体中的染色体，在此基础上选择染色体的编码和编码策略；定义适应度函数，作为对每个染色体进行评价的标准；随机生成初始种群；计算种群中个体的适应度；确定遗传策略，包括选择、交叉和变异算子作用于种群，产生新一代种群；如果新一代种群满足终止条件，则得到最优解或近似最优解，算法终止；否则返回前面第四步，再进行适应度计算，不断循环直到满足终止条件。
算例分析
（一）算例描述
已知广西省某第三方物流企业为某城市著名连锁超市负责农产品冷链配送业务。现已知该城市有2个生产基地、3种农产品、4个备选配送中心和7个连锁超市门店，为降低成本并快速响应市场需求，拟建2个配送中心。现要求设计一个农产品冷链物流配送网络的方案，满足配送总成本最小，以及连锁超市门店时间满意度和货运腐损度达到企业决策者的要求。具体数据如表1- 9所示。
（二）算例求解
本文使用Matlab和Lingo软件编程，进行算例求解和对比分析。其中遗传算法参数设置如下：种群规模N=40，最大遗传代数G=1000，交叉概率Pc=0.6，变异概率Pm=0.1，选择概率Ps=0.1。通过软件编程多次求解和运算，得到最优解为4985070元，结果如图2和图3所示。通过Matlab和Lingo软件，对数据进行多次运算和求解，顺利得出运行结果。
对不同模糊可行度水平的情况展开分析，通过软件运行求解得出不同的求解结果。不同模糊可行度下（S0=0.9和R0=0.4）对应的农产品冷链物流成本和选址结果如表10所示，不同模糊可行度、连锁超市门店满意度以及货运腐损度的农产品冷链物流成本和配送中心的运算结果如表11所示。
由表10可知，当连锁超市门店满意度和货运腐损度一定，随着模糊可行度增大，农产品冷链物流总成本大致增大，这是因为随着模糊可行度水平的增大，为了保证物流配送的可靠性，相应的总成本也会逐渐增大。由表11可知，当模糊可行度一定，随着连锁超市门店满意度越大和货运腐损度越小，农产品冷链物流承担的总成本会越大，这是因为效益背反原理，即物流的服务水平越好，相应的物流成本也就会越大。
结论
本文针对不确定环境下农产品冷链物流网络设计问题，在考虑不确定性、易腐性和时效性等因素对物流网络影响的基础上，提出了一个多源、多品种、多目标农产品冷链物流网络的模糊数学规划模型。本文在研究中仅考虑了农产品市场供需的不确定，而物流网络中其它多种不确定因素未进行考虑。同时，数学模型考虑的连锁超市门店时间满意度函数为普通的线性函数，时间敏感系数都取1，而拟合程度更高的满意度函数有待进一步研究。货运腐损度函数中的腐败速率系数统一取0.015，不同产品的腐败速率系数未进行考虑。因此在今后的研究中，将进一步研究拟合度更高的满意度函数和采用不同农产品的腐败速率系数。另外，在对多目标模型进行算法求解中，随着生产地数量、产品种类、备选配送中心的数量和连锁超市门店数量的增多，传统的求解方法可能将找不到最优解，故应进一步探讨更好的算法进行求解。
参考文献：
1.Zhou J，Liu B，New stochastic models for capacitated location-allocation problem[J].Computer Industrial Engineering，2003（45）
2.Omar Ahumada，J Rene Vilalobos，A Nicholas Mason.Tactical planning of the production and distribution of fresh agricultural products under uncertainty[J].Agricultural systems，2012（12）
3.崔广彬，李一军.模糊需求下物流系统CLRIP问题研究[J].控制与决策，2007（22）
4.陈鑫，汪传旭，石刘红.模糊随机需求下应急救援中心排队选址模型及算法[J].上海海事大学学报，2011（32）
5.毕娅，李文锋.基于协同库存和模糊需求的离散选址模型研究[J].统计与决策，2011（6）
6.陈鑫，汪传旭.模糊随机需求下应急救援中心选址优化模型[J].运筹与管理，2012（21）
7.周秀秀.模糊需求下的设备选址问题的求解[D].长安大学，2013
8.孙玮珊，杨斌.基于模糊数学的不确定性绿色物流网络设计[J].合肥工业大学学报，2014（37）
9.何静，张歆祺，宗传宏.连锁超市生鲜食品冷链物流网络构建与优化研究[J].广东农业科学，2011（22）
10.丁雪峰，汪莉亚.基于时间约束的多品种冷链共同配送模型[J].物流技术，2013（7）
11.宋效中，石钢.基于时效性的冷链配送中心选址问题[J].物流技术，2014，33（7）
12.陈淑姣.基于连锁超市门店价值和时间满意度的企业物流配送网络规划研究[D].重庆大学，2014
13.Jimenez M，Arenas M，Bilbao A，etc.Linear programming with fuzzy parameters：An interactive method resolution[J].European Journal of Operational Research，2007（177）
14.房少梅.数学建模理论、方法及应用[M].科学出版社，2014
15.雷英杰，张善文等.Matlab遗传算法工具箱及应用[M].西安电子科技大学出版社，2005